시간 복잡도와 공간 복잡도

Pdev37 2024. 4. 30. 17:59

2024. 4. 30. 17:59

시간 복잡도와 공간 복잡도

💡 알고 리즘이 얼마나 효율적인지 측정하는 기준

시간복잡도

코드가 얼마나 빠르게 작동하는지를 나타내는 지표

시간복잡도가 커지면 코드는 느려지고 시간 복잡도가 낮아지면 코드는 빨라짐

공간 복잡도

코드가 얼마나 많은 메모리를 사용하는지 나타내는 지표

공간복잡도가 커지면 메모리를 많이 차지하고 낮아지면 적게 차지함

시간복잡도(Time-complexity)

💡 알고리즘에 사용되는 총 연산횟수

표기법

O (big O): 이것보단 빠를때
θ (theta): 똑같을때(O , omega)
Ω (omega): 이것보단 느릴때

→ 일반적으로 big O 표기법을 사용

이유: 알고리즘이 최악일때 어떤 성능을 지녔는지 판단해야 사용 유무 판단 가능

시간 복잡도 계산

시간복잡도 계산하기

count = 0 #연산 1번
for i in range(3): #연산 4번
	count += i
	O(1)

변수에 다른 시간 복잡도 계산

def func(N):
	count = 0 #1번
	for i in range(N):
		count += 1 #N번 계산
	
	return count #1번 계산

# 시간복잡도 = N+2
# Big O : O(N)

def func2(N):
	result = 0 #1번
	for i in range(1,N):
		for j in range(N):
			result += i+j #N*N번 계산
	
	return result #1번

#시간 복잡도 N^2 + 2
#Big-O : O(N^2)

def func2(N, M):
	result = 0 #1번
	for j in range(M): # O(M)
		result += j
	for i in range(N): # O(N^2)
		for j in range(N):
			result += i+j #N*N번 계산
	
	return result #1번

#Big-O : O(N^2 + M)

대표적인 시간 복잡도

O(1) : 상수 시간
- 입력값 n 이 주어졌을 때, 알고리즘이 문제를 해결하는데 오직 한 단계만 거칩니다.

O(log n) : 로그 시간

입력값 n 이 주어졌을 때, 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듭니다.

       O
      / \\
     *O*   O
    /\\   /\\
   *O*  O O  O
  /\\ /\\ /\\ /\\
 *O* OO OO O O O

log_2 16 = 4

O(log_2 2^N) => log_2 X = log_10 X / log_10 2 = log_10 X

N = 5
| 1 | 2 | 3 | 4 | 5 | 5
| 2 | 3 | 4 | 5 | 0 | 4
| 3 | 4 | 5 | 0 | 0 | 3
...
5 + 4 + .. + 2 + 1
=> N(N+1)/2 -> N^2+N -> O(N^2)

O(n) : 직선적 시간
- 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가집니다.
O(n^2) : 2차 시간
- 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱입니다.
O(C^n) : 지수 시간
- 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱입니다.

시간복잡도의 중요성

	코드1	코드2
시간 복잡도	1,000N	2N*2
Big-O	O(N)	O(N^2)

N1101001,00010,000

N	1	10	100	1,000	10,000
코드1	1,000	10,000	100,000	1,000,000	10,000,000
코드2	2	200	20,000	2,000,000	200,000,000

N의 크기에 따라 시간 복잡도의 변화 수준이 다름

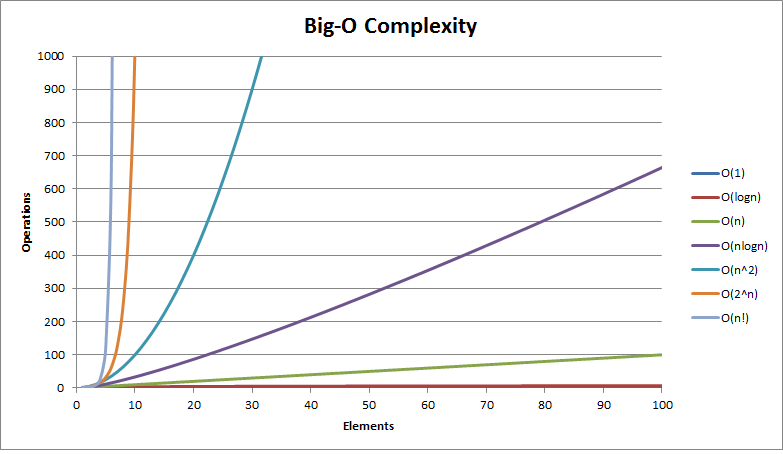
→ N의 크기에 맞게 알고리즘을 잘 설계 해야함

공간복잡도(Space-complexity)

알고리즘에 사용되는 메모리 공간의 총량

⇒ 굉장히 중요했지만 기술의 발전으로 메모리가 늘어나면서 중요도가 떨어짐

Big-O 공간복잡도

a = 1
#bigO 공간복잡도 =O(1)

a = [N for i in N]
#bigO 공간복답도 = O(N)

a = [[N for i in N] for j in  N]
#BigO 공간복잡도 = O(N^2)

→ 시간복잡도와 공간복잡도는 tradeoff가 일어남

→ 공간 복잡도 up 시간복잡도 down

Reference

https://celltong.tistory.com/entry/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EC%8B%9C%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84%EC%99%80-%EA%B3%B5%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84

Pdev Sec